Differentiation

Differential Calculus cuts something into small pieces to find how it changes.

Differentiation is the process of getting the derivative of a value.

The derivative of a function measures the sensitivity to change of the output value in response to changes in the input value.

• ex. the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.

the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.

• "at any infinitisemely small slice of time, by how much is variable A (e.g. speed)

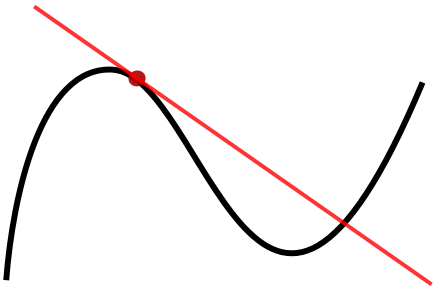
The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point

ex. imagine the following curvy line is a function describing the speed of a car over a period of time. Imagine the red dot takes place at $t=3$ seconds.

• the derivative of the function for when $t=3$ is the slope of the red line.

Example: Measuring speed at an instant

• source

Imagine we wanted to measure how fast we were driving at an exact instant in time. To calculate this, we use the equation:

$speed = {distance \over time}$

$speed = {0m \over 0s} = 0$

Our speed can't be calculated by this, because in order to measure speed, we need some distance and some time.

• Even the speedometer of a car just shows us an average of how fast we were going for the last (very short) amount of time.

So we try a different formula, which tells us the distance an object falls over a certain amount of time:

$d = 5t^2$

Which is a simplified version of:

$d = {1\over2}gt^2$

But this doesn't work either, because at $t = 0$, our $d$ results in $0$.

So to solve this problem, we invent a time so short that it won't matter, and we call it $Δt$. Now, we figure out the difference in distance between $t$ and $t + Δt$.

At 1 second:

$d = 5(1)^2 = 5m$

At $1 + Δt$ seconds:

$d = 5(1 + Δt)^2$

Expanding,

$d = 5 \times (1 + Δt)(1 + Δt)m$

$d = 5 \times (1 + 2Δt + Δt^2)m$

$d = (5 + 10Δt + 5Δt^2)$

So between 1 second and (1+Δt) seconds we get:

$Δd = (5 + 10Δt + 5Δt^2) - 5m$

And change in distance over time:

$Δd/t = {(5 + 10Δt + 5Δt^2) - 5m \over Δt}$

$Δd/t = 10 + 5Δt$

So the speed is $10 + 5Δt m/s$, but then we want $Δt$ to be so small that it doesn't matter, so we substitute in zero (an infinitely small number would be inconsequential to the calculation anyway)

Therefore, the speed is exactly $10m/s$

---

Backlinks

• Calculus
• Integration