Trigonometry

The interior angles of a triangle always add up to 180°

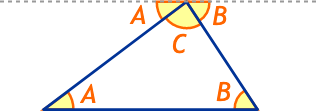
• angles A are the same
• angles B are the same

the area of any polygon can be found by dividing the polygon into triangles.

• see: Polygon Triangulation
• For shapes with curved boundary, calculus is usually required to compute the area.

Right Triangles

The interesting thing about right triangles is that they are one half of a rectangle.

• therefore, anything that can be figured out with a rectangle can also be figured out with a right triangle
  • ex. area of a rectangle is $H \times W$, area of right triangle is ${H \times W} \over 2$

Pythagorean theorem

The theory states that the area of the square on the side of the hypotenuse ($c$) is equal to the area of $b + c$

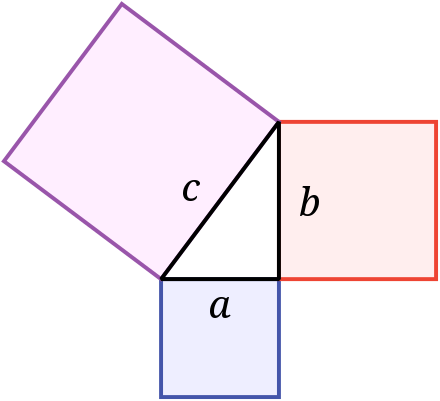
Therefore, with this formula, given the lengths of 2 sides we can find the length of the 3rd.

This formula can also be used to determine if an angle is truly 90°. Simply measure the length of each side and plug it in to the formula to see if both sides equal each other.

Sine, Cosine, Tangent

purpose: given an angle and length of a side of a right triangle, get the other side

The main functions in trigonometry are Sine, Cosine and Tangent

• each function is simply one side of a right-angled triangle divided by another.
• Their general rule is when we know any 3 of the sides or angles, we can find the other 3 (except for the three angles case)

The triangle can be large or small and the ratio of sides stays the same. Only the angle changes the ratio.

Sine

Sine is the ratio of $Opposite \over Hypotenuse$

• ex. when doing a Sine calculation, 45° results in 0.7071. This number represents the ratio of the side lengths, which would mean that the Opposite is about 0.7071 times as long as the Hypotenuse.

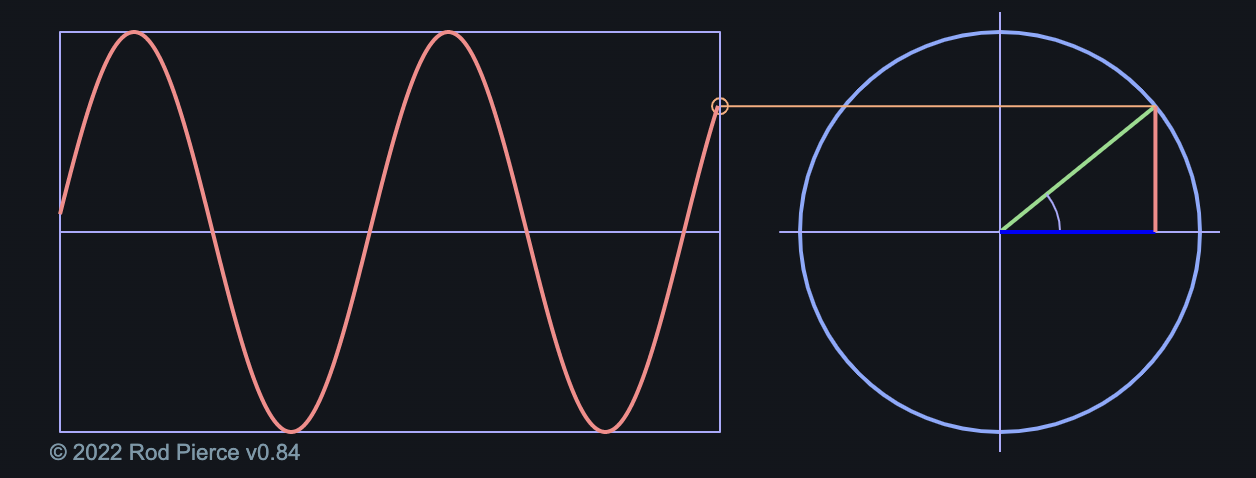
• image: creation of a sine wave

Arcsine, Arccosine, Arctangent (inverse trig functions)

purpose: given the lengths of 2 sides of a right triangle, get the angle

While the sine function takes an angle and returns the ratio of $opposite / hypotenuse$, arcsine (ie. inverse sine) takes a ratio and returns the angle.

• ie. If the sine of 30° is 0.5, then the arcsine of 0.5 is 30°:

Cotangent, Secant, Cosecant

Like Sine, Cosine and Tangent, these functions all involve dividing one side by another

• secant is equal to 1 divided by cos
• cosecant is equal to 1 divided by sin
• cotangent is equal to 1 divided by tan