Linear Algebra

Matrix Multiplication

Matrix multiplication is multiplying one matrix by another matrix

Rules

To multiply two matrices, the number of columns of the 1st matrix must equal the number of rows of the 2nd matrix.

visualized a different way, to multiply two matrices the inner dimensions must match.
- $(3, 2) @ (2, 3)$ indicates 2 matrices, the first of which has 3 arrays of size 2, while the second has 2 arrays of size 3. Here, the inner values (ie. those closest to the @) are $2$ , so this works. By the same token, $(2, 3) @ (2, 3)$ won't work because the inner values ( $3$ and $2$ ) are not the same. To be able to multiply either of these matrices, we'd have to transpose one of them.

The result of the calculation will have the same number of rows as the 1st matrix, and the same number of columns as the 2nd matrix.

visualized a different way, the resulting matrix will have the shape of the outer dimensions
- $(2, 3) @ (3, 2)$ will result in a matrix with dimensions $(2, 2)$

How it works

To derive the result, we need to do the dot product of rows and columns.

ex. for a single row and single column, we would get the result like this:

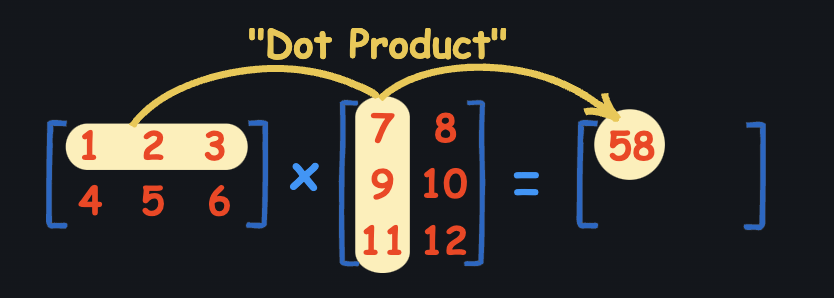
Because:

$(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58$

For a matrix such as this, we need to multiply the following combinations:

row 1 • column 1
row 1 • column 2
row 2 • column 1
row 2 • column 2

Unlike multiplication of scalars, matrix multiplication is not commutative

this means that AB ≠ BA

Pytorch example

tensor1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
tensor2 = torch.tensor([[7, 8], [9, 10], [11, 12]])
new_tensor = torch.matmul(tensor, tensor2)
# tensor([[ 58,  64],
#         [139, 154]])

Why do we calculate like this?

There has to be some relation between the 1st and 2nd matrix.

ex. the 1st matrix represents units of fruit sold (broken down by fruit type) and the 2nd matrix represents the cost per fruit type

If we consider it like this, then we need to add up all the "total values" of the sales of each fruit. How we do this is by multiplying each individual fruit price by the quantity of that price sold, then performing the same operation for each fruit, and finally adding them all up:

Apple pie value + Cherry pie value + Blueberry pie value

$3×13 + $4×8 + $2×6 = $83

Identity Matrix

An identity matrix is the equivalent of $1$ , when it comes to identity multiplication

that is, when we multiply X by 1, the answer is X. In the same way, if we multiply Matrix Y by the identity matrix, the answer is Matrix Y

IdentityMatrix = [
    [ 1, 0, 0 ]
    [ 0, 1, 0 ]
    [ 0, 0, 1 ]
]

The identity matrix can be any row/column length, as long as it follows the pattern of diagonal ones from top left to bottom right.

E Resources

https://www.mathsisfun.com/algebra/matrix-multiplying.html

UE Resources

3Blue1Brown series on Linear Algebra

Resources

Visualizing matrix multiplication

Children