Set Theory

Overview

A set is basically a grouping of unique (ie. no duplicate) things (called members, or elements)

• ex. numbers, fruit, other sets, functions.
• ex. The deck of cards is a set, whose elements are the cards

Sets can be finite or infinite. For example, {1, 2, 5, 6} is a finite set. The set of all the natural numbers is an infinite set.

ordering and duplication of elements is irrelevant

• ex. ${2, 4, 6}$ and ${4, 6, 4, 2}$ represent the same set.

Sets correspond to general.lang.types (Private) in programming languages very well. For example:

• number type can be looked at as a set of all possible numbers
• string type is a set of all possible strings
• 'a' | 'b' | 'c' type corresponds to the {'a', 'b', 'c'} set
• null type is a singleton type with only one element, the null value (which happens to have the same name)
• undefined type is a singleton type with only one element, the undefined value (which happens to have the same name)

If $A$ is a set and $b$ is an element of $A$, we write $b \in A$

The number of elements of a set $A$ is denoted by $|A|$.

• ex. a set $P$ with 7 elements can be written: $|P|$ = 7; and its elements can be listed like so: $P = \{Alice, Bob, Carl, Diane, Eve, Frank, George\}$
  • here, we say "set $P$ has a cardinality of 7"

We can specify a set by a property that filters out some elements from a large universe (e.g. out of all real numbers, integers that are greater than 0)

• ex. $\{x \in \mathbb{Z} : x \ge 0\}$, which means "$x$ is part of the set of integers and is also greater than $0$".

Predetermined sets

For mathematics, various sets of numbers are important:

• the set of real numbers, denoted by $\mathbb{R}$;
• the set of rational numbers, denoted by $\mathbb{Q}$;
• the set of integers, denote by $\mathbb{Z}$;
• the set of non-negative integers, denoted by $\mathbb{Z+}$;
• the set of positive integers (ie. natural numbers), denoted by $\mathbb{N}$.
• the empty set, the set with no elements is another important (although not very interesting) set; it is denoted by $∅$.

Operations

In set theory, union and intersection are names of operations on sets.

• ex. The union of two sets is a set that contains all elements that appear in either set (ie. if the element appears in either set, then it's part of the union set).
• ex. The intersection of two sets is a set that only contains elements that are present in both sets.

Subset ($\subseteq$)

Set $A$ is called a subset of a set $B$ if every element of $A$ is also an element of $B$.

• denoted $A \subseteq B$.

the empty set ($∅$) is a subset of every set, and among the predetermined sets (above), we can say:

• $∅ ⊆ \mathbb{N} ⊆ \mathbb{Z+} ⊆ \mathbb{Z} ⊆ \mathbb{Q} ⊆ \mathbb{R}$

The number of subsets in a set is a power of 2: if the set has $n$ elements, the result is $2^n$

• ex. with a set with 2 elements $\{a, b\}$, we can have 4 subsets($2^2$): $∅$, $\{a\}$, $\{b\}$, $\{a,b\}$
• ex. with a set with 3 elements $\{a, b, c\}$, we can have 8 subsets($3^2$): $∅$, $\{a\}$, $\{b\}$, $\{a,b\}$, $\{b,c\}$, $\{c\}$, $\{a,b,c\}$, $\{a,c\}$

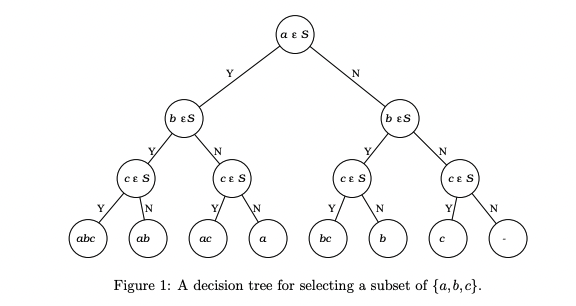
We read this figure as follows. We want to select a subset called S. We start from the circle on the top (called a node). The node contains a question: is a1 an element of S? The two arrows going out of this node are labeled with the two possible answers to this question (Yes and No). We make a decision and follow the appropriate arrow (also called an edge) to the the node at the other end. This node contains the next question: is a2 an element of S? Follow the arrow corresponding to your answer to the next node, which contains the third (and in this case last) question you have to answer to determine the subset: is a3 an element of S? Giving an answer and following the appropriate arrow we get to a node, which contains a listing of the elements of S. Thus to select a subset corresponds to walking down this diagram from the top to the bottom. There are just as many subsets of our set as there are nodes on the last level.